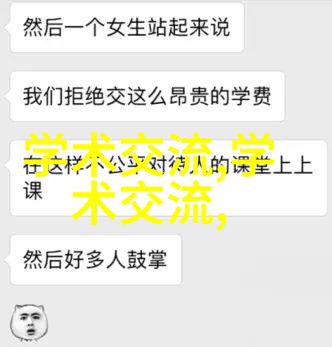
在工科领域，人们常常会被一个概念所困扰：三维空间中的物体具有6个自由度。想象一下这样一个场景：

图中展示的是右手坐标系，这六个自由度分别是沿着X、Y、Z三个轴的直线移动，以及绕这三个轴旋转。然而，这一概念往往导致误解：以为机床必须拥有6个自由度或6个轴才能实现任意角度加工。但事实并非如此。

传统的三轴机床在处理复杂表面和多孔结构时，需要使用特殊夹具，并且可能需要进行多次加工步骤。而五轴联动数控机床则能够在单次装夹下完成高速、高精密的复杂形状加工。

关键在于刀具（或测头）的灵活性，它们可以从任何方向接近工作件，从而实现任意角度加工。这涉及到如何描述刀具（或测头）的位置和姿态。

三轴数控机床只能通过X、Y、Z三个直线运动来改变刀具（或测头）的位置，而其姿态是固定的。在五轴机床中，由于额外两个旋转轴的加入，刀具（或测头）的位置和姿态都能变化。我们用“刀锥矢量”这一术语来描述这些变化。

这个矢量是一个单位向量，它代表了刀具（或测头）相对于工作件的方向。由于它是一个球面上的点，我们可以通过两种方式来描述这个点——经纬度或者笛卡尔坐标。这两种方法各自包含两个独立变量，即对应于两个自由度。

因此，只需在三维空间中添加两个旋转軸，就能实现任意方向切割。这就是为什么五軸聯動數控機床比傳統的三軸機床更為先進，它們擁有額外兩個軸，這些額外兩個軸允許工具進行複雜形狀工件的快速高精確切割。

最后要澄清的是，与飞行器类似地使用欧拉角描述飞行器姿态不同，在讨论刀锥矢量时，我们只需考虑俯仰和偏航即可，因为翻滚角并不影响结果。此外，由于翻滚不影响最终结果，因此我们只需考虑俯仰和偏航这两个独立变量就足够了。

希望上述内容能够帮助读者理解这方面的问题。如果你还有其他疑问，请随时提问！